介绍
归并算法指的是将两个顺序序列合并成一个顺序序列的方法。
假设开始有数列 {6,202,100,301,38,8,1} 需要按照从小到大的顺序进行重新排列;
-
初始单个数:6, 202, 100, 301, 38, 8, 1
-
第一次归并:{6, 202}, {100, 301}, {8, 38}, {1},本轮比较的次数:3;
-
第二次归并:{6, 100, 202, 301}, {1, 8, 38},本轮比较次数:4;
-
第三次归并:{1, 6, 8, 38, 100, 202, 301},本轮比较次数:4;
总的比较次数为:3 + 4 + 4 = 11;
原理
单次归并过程
-
申请空间(大小为两个已经排序序列之和,该空间用来存放合并后的序列);
-
设定两个指针,最初位置分别为两个已经排序序列的起始位置;
-
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
-
重复步骤 3 直到某一指针超出序列尾;
-
将另一序列剩下的所有元素直接复制到合并序列尾;
图解单次归并
下图以长度分别为 4、4 的已排序序列的归并过程进行演示:
第二行红框是申请的空间,用来存放合并后的序列;
红色箭头是设定的两个指针,初始分别指向两个序列的起始位置;
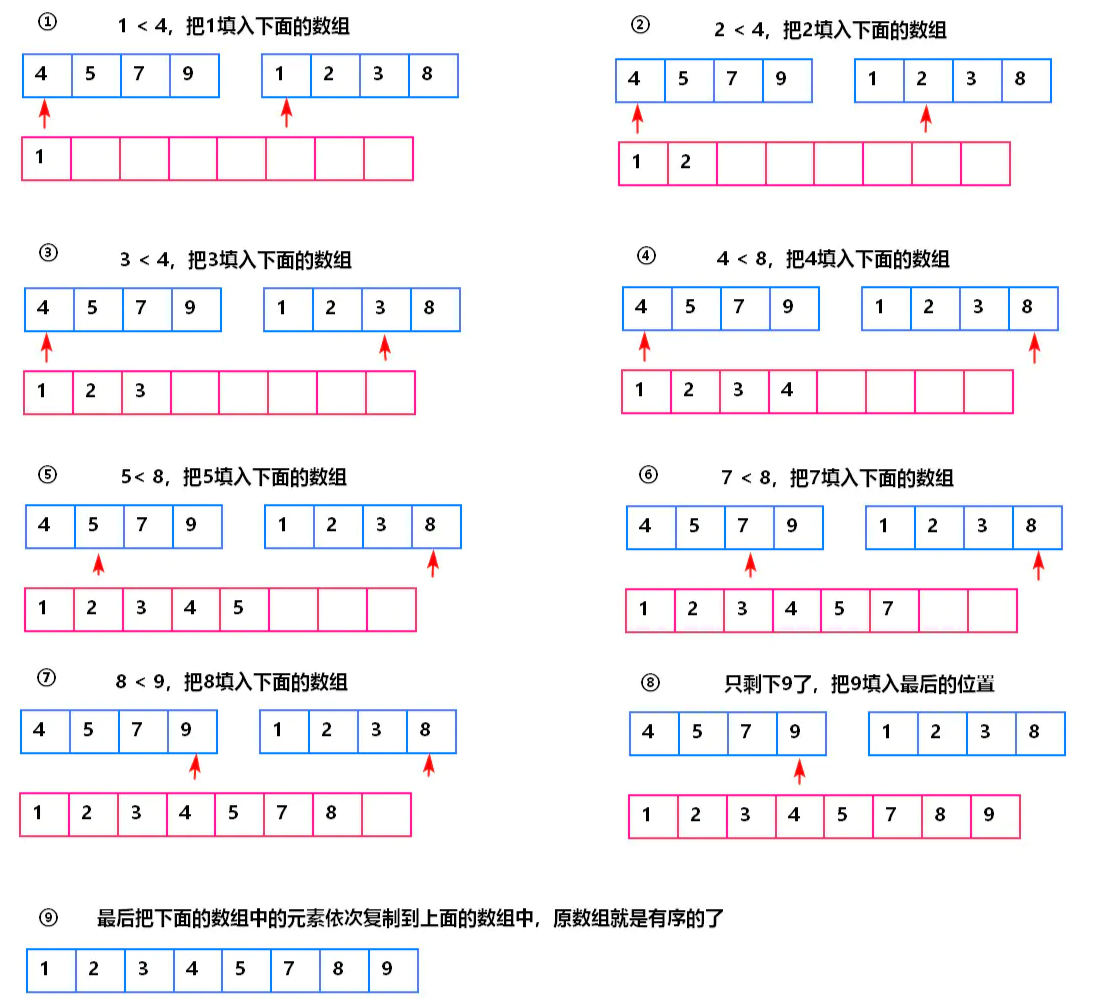
示例
c 语言归并算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <stdlib.h>
#include <stdio.h>
void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex)
{
int i = startIndex, j=midIndex+1, k = startIndex;
while(i!=midIndex+1 && j!=endIndex+1) {
if(sourceArr[i] > sourceArr[j])
tempArr[k++] = sourceArr[j++];
else
tempArr[k++] = sourceArr[i++];
}
while(i != midIndex+1)
tempArr[k++] = sourceArr[i++];
while(j != endIndex+1)
tempArr[k++] = sourceArr[j++];
for(i=startIndex; i<=endIndex; i++)
sourceArr[i] = tempArr[i];
}
/* 内部使用递归 */
void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex)
{
int midIndex;
if(startIndex < endIndex) {
midIndex = startIndex + (endIndex-startIndex) / 2; /* 避免溢出 int */
MergeSort(sourceArr, tempArr, startIndex, midIndex);
MergeSort(sourceArr, tempArr, midIndex+1, endIndex);
Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
}
}
int main(int argc, char * argv[])
{
int a[8] = {50, 10, 20, 30, 70, 40, 80, 60};
int i, b[8];
MergeSort(a, b, 0, 7);
for(i=0; i<8; i++)
printf("%d ", a[i]);
printf("\n");
return 0;
}